A integral definida pode ser usada para muitas coisas nas ciências naturais e engenharias.
Trabalho realizado por uma força
Utilizada para situações onde a força F permanece constante durante todo o deslocamento.
Como sabemos, por definição, que o trabalho é a força multiplicada pelo deslocamento, se considerarmos cada vez menor os subintervalos de deslocamento e somarmos, estamos fazendo nada mais do que uma integral da função  .
.
 .
.
Considere uma força sendo aplicada sobre um corpo, que varia conforme um deslocamento x num intervalo [a,b]. O trabalho W realizado por  será:
será:
 será:
será:Valor Médio de uma função
Em casos onde se deseja saber o valor médio de uma variável tendo uma quantidade finita de termos é fácil calcularmos seu valor médio. Por exemplo, têm-se 24 leituras de temperatura, 1 para cada hora do dia. Então, a temperatura média será a soma da temperatura de cada hora dividido por 24. Mas, e em situações onde se tem infinitas possibilidades de leitura, ou seja, não apenas pontos no gráfico, mas uma curva? A integral pode nos ajudar.
Para valores inteiros, tínhamos como média:
para um intervalo fechado [a,b]
Para valores reais, também teremos como média:
para um intervalo fechado [a,b]
Dividiremos esse intervalo [a,b] em n subintervalos iguais, cada um com comprimento Δx, sendo:
Mas,
Substituindo n na equação do valor médio:
Aplicando o limite quando n tende ao infinito, chegamos ao valor médio de f no intervalo [a,b]:
Volume de um sólido de revolução
Um sólido de revolução é um sólido gerado pela rotação de uma região plana em torno de uma reta que está no mesmo plano da região; a reta é denominada eixo de revolução.
- Rotacionando um retângulo em um eixo, obtém-se um cilindro circular reto;
- Rotacionando um círculo em um eixo, obtém-se uma esfera;
- Rotacionando um triângulo em um eixo, obtém-se um cone;
Estes sólidos são os mais comuns e fáceis de se calcular o volume, uma vez que suas fórmulas para isso já estão construídas.
E se tivermos um sólido no espaço sem formas bem definidas, como calculamos seu volume? O cálculo integral pode nos ajudar, vamos às demonstrações.
Exemplo 1 Observe os gráficos
Fonte: GeoGebra Tube
Autor: Instituto GeoGebra de Celaya
Os dois gráficos são iguais, mas o da direita é a curva f(x) revolucionada em um eixo no espaço cartesiano. No gráfico em 2D estimamos a área abaixo da curva por retângulos, no 3D podemos estimar por cilindros. Perceba que f(x) agora é o valor do raio do cilindro, e não mais da altura de um retângulo. Além disso, o Δx, que antes era a base dos retângulos, agora é a altura de cilindro.
Então, o volume do cilindro pode ser expresso por:
Agora entra em cena algo que já vimos bastante em outras seções de integrais do site. Quanto mais cilindros colocarmos dentro do sólido, mais precisa nossa estimação ficará.
Vamos estimar o volume do sólido gerado pela revolução da função f(x) = x² no intervalo [0,2] através do volume de 10 cilindros, considerando como valor do raio do i-ésimo cilindro o valor do vértice inferior esquerdo de cada retângulo aplicado na função f.
Como serão 10 cilindros, cada um terá como altura 2/10 = 0,2
Os vértices inferiores esquerdos dos retângulos estão na sequência finita: (0; 0,2;...;1,8), portanto, os os raios dos cilindros serão a sequências também finita: [f(0); f(0,2);...; f(1,8)].
E como obtemos o volume exato desse sólido?
Da mesma maneira que fizemos com as áreas de figuras no plano cartesiano. Se tendermos o número de cilindros ao infinito, Δx se torna infinitesimalmente pequeno, chegando à uma integral simples:
Que no caso do problema que estamos investigando ficaria:






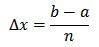












Nenhum comentário:
Postar um comentário