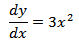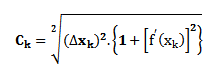Aplicação 1: Estudo do comportamento crescente/decrescente de uma função
Quando analisamos a derivada para determinar o comportamento de (de)crescimento uma função, temos três situações:
Se f é crescente em [a, b], então f ' > 0 em [a, b];
Se f é decrescente em [a, b], então f ’ < 0 em [a, b];
Se uma função f possui valores de máximo ou mínimo local em um ponto x = a de seu domínio, então f '(a) = 0.
Em resumo:
Tomemos como exemplo o gráfico da função abaixo:
Figura 2. Máximos e mínimos de uma função polinomial de grau 3.
A partir da observação gráfica podemos concluir que:
O ponto de abscissa x = -2 (Ponto A) é um máximo local; então f '(x) > 0 para x < -2 e f '(x) < 0 para x > -2;
O ponto de abscissa x = 8 (Ponto B) é um mínimo local; então f '(x) < 0 para x < 8 e f '(x) > 0 para x > 8.
No intervalo [-6, 14] temos:
O ponto de abscissa x = 8 é um mínimo global, pois a função não assume valores menores que f(8) para este intervalo;
O ponto de abscissa x = 14 é um máximo global, pois a função não assume valores maiores que f(14) para este intervalo.
Se existe um ponto de abscissa x0 na função na qual f ' = 0 ou f ' não existe, dizemos que o ponto (x0,f(x0)) é um ponto crítico.
Exemplo 1
y = x²
Derivando, temos que:
Como para os pontos críticos temos que a derivada é zero, então:
2x = 0
x = 0
Desta forma, concluímos que o ponto de abscissa x = 0 é um ponto crítico. Para analisarmos se tal ponto é um ponto de máximo ou de mínimo, faremos o chamado teste da derivada primeira, que consiste, basicamente, em analisar o comportamento da função f '(x) nos pontos anteriores e posteriores ao ponto crítico.
Teste da derivada primeira
Tendo o ponto de abscissa x = 0 como um ponto crítico, podemos analisar o comportamento da derivada para x < 0 e para x > 0.
Sendo 
, temos que para x < 0,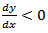 
e, portanto, que a função apresenta comportamento decrescente à esquerda de x = 0.
Para x > 0 temos que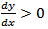 
e, portanto, a função apresenta comportamento crescente para valores maiores que x = 0.
Dessa forma, podemos concluir que o ponto de abscissa x = 0 é um mínimo local.
Veja um exemplo aplicado aqui no contexto de otimização.
Veja outro exemplo em um contexto físico.
Exemplo 2
y = x³
Derivando obtemos que:
Para os pontos críticos temos que a derivada é igual a zero, portanto:
3x² = 0
x² = 0
x = 0
Desta forma, o ponto de abscissa x = 0 é um ponto crítico. Para determinar se o ponto de abscissa x = 0 é um ponto de máximo ou um ponto de mínimo, ou apenas um ponto crítico aplicamos o teste da derivada primeira.
Teste da derivada primeira
Sendo 
e x = 0 o ponto crítico, analisaremos o comportamento da derivada de f(x) para valores menores que x = 0 e para valores maiores que x = 0. Nota-se aqui que, como a variável x está elevada a um expoente par,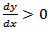 
para todo x ≠ 0.
Desta forma, a função é estritamente crescente e, portanto, o ponto de abscissa x = 0 não é mínimo nem máximo local.
Exemplo 3
y = √x
Derivando, obtemos que:
Novamente, para determinação dos pontos críticos igualamos a derivada a zero, desta forma:
Observamos que não existe um valor de x para o qual a derivada se anula, porém, nota-se que para x = 0 a função f '(x) não existe, o que caracteriza o ponto de abscissa x = 0 como um ponto crítico. Aplicando o teste da primeira derivada, nota-se que:
Lê-se: a derivada de y em relação a variável x é positiva para todo x pertencente aos reais positivos, com exceção do ponto de abscissa x = 0. Portanto, a função y = √x é estritamente crescente.
Exemplo 4 Considere a função f(x) = x³ - 9x² - 48x + 52
Como f é um polinômio cúbico, esperamos um gráfico com um formato semelhante ao de um S. Podemos usar a derivada para determinar onde a função é crescente e onde ela é decrescente. A derivada de f é:
f'(x) = 3x² - 18x - 48
Para determinar onde f ' > 0 ou f ' < 0, começaremos por determinar onde f ' = 0. Fatorando f ' em 3(x+2)(x-8) = 0, temos que x = -2 ou x = 8. Como f ' = 0 apenas em x = -2 e em x = 8 e como f ' é contínua, f ' não pode mudar de sinal em nenhum dos três intervalos x < -2, ou -2 < x < 8, ou 8 < x. Como f'(-3) = 33 > 0, reconhecemos que f ' é positiva para x < -2, e assim que f é crescente para x < -2. Analogamente, f '(0) = -48 e f '(10) = 72, então f decresce se -2 < x < 8 e cresce para x > 8. Resumindo,
Calculamos que f(-2) = 104 e f(8) = -396. Então, no intervalo -2 < x < 8, a função decresce de 104 para -396. Há ainda outro ponto no gráfico, fácil de trabalhar: é a interseção com o eixo dos y, f(0) = 52. Com esses três pontos, desenhamos o gráfico de f.
Se uma função f possui valores de máximo ou mínimo local em um ponto x = a de seu domínio, então f '(a) = 0.
Em resumo:
Figura 2. Máximos e mínimos de uma função polinomial de grau 3.
y = x²
2x = 0
x = 0
, temos que para x < 0,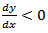 
e, portanto, que a função apresenta comportamento decrescente à esquerda de x = 0.
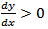e, portanto, a função apresenta comportamento crescente para valores maiores que x = 0. Veja um exemplo aplicado aqui no contexto de otimização.
Veja outro exemplo em um contexto físico.
y = x³
3x² = 0
x² = 0
x = 0
e x = 0 o ponto crítico, analisaremos o comportamento da derivada de f(x) para valores menores que x = 0 e para valores maiores que x = 0. Nota-se aqui que, como a variável x está elevada a um expoente par,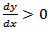 
para todo x ≠ 0.
y = √x
Derivando, obtemos que:
Exemplo 4 Considere a função f(x) = x³ - 9x² - 48x + 52
Como f é um polinômio cúbico, esperamos um gráfico com um formato semelhante ao de um S. Podemos usar a derivada para determinar onde a função é crescente e onde ela é decrescente. A derivada de f é:
f'(x) = 3x² - 18x - 48
Para determinar onde f ' > 0 ou f ' < 0, começaremos por determinar onde f ' = 0. Fatorando f ' em 3(x+2)(x-8) = 0, temos que x = -2 ou x = 8. Como f ' = 0 apenas em x = -2 e em x = 8 e como f ' é contínua, f ' não pode mudar de sinal em nenhum dos três intervalos x < -2, ou -2 < x < 8, ou 8 < x. Como f'(-3) = 33 > 0, reconhecemos que f ' é positiva para x < -2, e assim que f é crescente para x < -2. Analogamente, f '(0) = -48 e f '(10) = 72, então f decresce se -2 < x < 8 e cresce para x > 8. Resumindo,
Aplicação 2: Como a função cresce/decresce?
- Se y’ é crescente em [a, b], então o gráfico de f é côncavo para cima em [a, b] . Ou seja, y ’’ > 0 (que representa a derivada segunda de f);
- Se y’ é decrescente em [a, b], então o gráfico de f é côncavo para baixo em [a,b]. Ou seja, y ’’ < 0 nesse intervalo.
A chamada derivada de 2a ordem, y’’, também pode ser representada por:
Dizemos que um ponto é um ponto de inflexão quando o gráfico possui uma reta tangente onde há mudança de concavidade. Ou seja, um ponto tal que exista f ' e f " = 0.
- Se y’ é crescente em [a, b], então o gráfico de f é côncavo para cima em [a, b] . Ou seja, y ’’ > 0 (que representa a derivada segunda de f);
- Se y’ é decrescente em [a, b], então o gráfico de f é côncavo para baixo em [a,b]. Ou seja, y ’’ < 0 nesse intervalo.
A chamada derivada de 2a ordem, y’’, também pode ser representada por:
Dizemos que um ponto é um ponto de inflexão quando o gráfico possui uma reta tangente onde há mudança de concavidade. Ou seja, um ponto tal que exista f ' e f " = 0.
Aplicação 3: Aproximação linear local
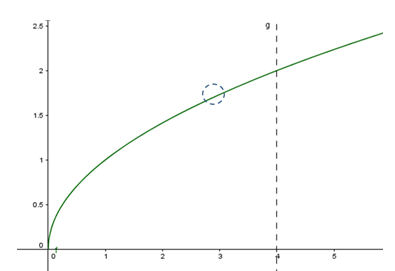
Podemos aproximar o valor de f(x) por meio da reta tangente em x = a para valores próximos de x = a.
Tomemos como exemplo a função 
Como 
, então:
, então:
Sendo assim, em x = 4:
Podemos determinar, portanto, a equação da reta tangente ao ponto (4, f(4)).
Como podemos observar nos gráficos abaixo, nas proximidades do ponto de abscissa x = 4 os valores da função f(x) são muito próximo dos valores dados pela equação da reta tangente ao ponto de abscissa x = 4.
Figura 1. Valores de y nas proximidades de x = 4 para f(x) e a f '(x) a este ponto.
Podemos, portanto, estimar o valor da função em um ponto próximo de x = 4. Por exemplo, para o ponto de abscissa x = 4,17:
Com o auxílio de uma calculadora, verificamos que 
e que, portanto, é possível aproximar o valor de f(x) por meio da reta tangente em x = a para valores próximos de x = a.
e que, portanto, é possível aproximar o valor de f(x) por meio da reta tangente em x = a para valores próximos de x = a.Aplicação 4: Derivadas para calcular limites
Podemos, também, utilizar o fato de que f e g são diferenciáveis e g'(a) ≠ 0 em um intervalo aberto contendo x = a, então a expressão 
pode ser reescrita utilizando as equações das retas tangentes em x = a. Se f(a) = g(a) = 0, então:
Esse resultado, conhecido como regra de L'Hôpital, pode ser aplicado se 
ou 
. Daí,
, se o limite do lado direito existir, ou for +∞ ou -∞.
Exemplos
Podemos, também, utilizar o fato de que f e g são diferenciáveis e g'(a) ≠ 0 em um intervalo aberto contendo x = a, então a expressão
pode ser reescrita utilizando as equações das retas tangentes em x = a. Se f(a) = g(a) = 0, então:
Esse resultado, conhecido como regra de L'Hôpital, pode ser aplicado se
ou 
. Daí,
, se o limite do lado direito existir, ou for +∞ ou -∞.Exemplos
Aplicação 5: Comprimento de um arco
A integral é uma importante ferramenta quando se deseja determinar o comprimento de regiões ou pedações do gráfico de uma curva y = f(x) num intervalo [a, b]. Para isso é necessário assumirmos que a função f(x) é lisa, ou seja, que sua derivada, f'(x), é contínua no intervalo [a, b].
Novamente, a estratégia a ser utilizada é a “quebra” da curva em segmentos pequenos a ponto desses poderem ser aproximados por segmentos de retas.
A região da curva obtida será aproximada pelo comprimento da hipotenusa de um triângulo retângulo de catetos 
. Portanto:
Sabemos que a tangente deste mesmo retângulo nos fornece a taxa de variação (derivada) da função para este intervalo, ou seja, 
. Manipulando esta relação, tem-se:
Então,
Removendo o termo 
da raiz obtemos que:
Somando-se os comprimentos de todos os n arcos obtém-se uma nova soma de Riemann. Fazendo o número de subintervalos se aproximar do infinito, obtém-se o comprimento de arco de uma função lisa do tipo y = f(x) no intervalo [a, b].
Tomemos como exemplo a função y = 2x no intervalo [1,3]. Sua derivada será y' = 2 e o comprimento do arco formado pelo gráfico para este intervalo será dado por:
A integral é uma importante ferramenta quando se deseja determinar o comprimento de regiões ou pedações do gráfico de uma curva y = f(x) num intervalo [a, b]. Para isso é necessário assumirmos que a função f(x) é lisa, ou seja, que sua derivada, f'(x), é contínua no intervalo [a, b].
Novamente, a estratégia a ser utilizada é a “quebra” da curva em segmentos pequenos a ponto desses poderem ser aproximados por segmentos de retas.
A região da curva obtida será aproximada pelo comprimento da hipotenusa de um triângulo retângulo de catetos . Portanto:
Sabemos que a tangente deste mesmo retângulo nos fornece a taxa de variação (derivada) da função para este intervalo, ou seja, 
. Portanto:
. Manipulando esta relação, tem-se:
da raiz obtemos que:
Tomemos como exemplo a função y = 2x no intervalo [1,3]. Sua derivada será y' = 2 e o comprimento do arco formado pelo gráfico para este intervalo será dado por:
