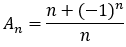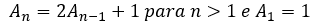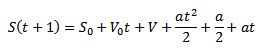O que é uma sequência
Uma sequência é uma lista infinita de números S1, S2, S3, ..., Sn, .... Denominamos S1 o primeiro termo, S2 o segundo termo e Sn o termo geral.Exemplo 1 Gere os seis primeiros termos das sequências a seguir:
(a)
(b) 
Substituindo n = 1, 2, 3, 4, 5 e 6 na fórmula do termo geral de (a), obtemos:
1, 3, 6, 10, 15 e 21.
Substituindo n = 1, 2, 3, 4, 5 e 6 na fórmula do termo geral de (b), obtemos:
0, 3/2, 2/3, 5/4, 4/5 e 7/6.
As sequências numéricas são funções de domínio real e contradomínio um conjunto qualquer não vazio.
As progressões aritméticas são um caso particular de sequência que possuem um valor constante de um número para outro, chamado razão, a partir do seu segundo termo.²
Neste gráfico você pode manipular uma progressão aritmética. Altere n, r e a1 e gere diferentes gráficos. Ative-os nos quadrados em branco.
Fonte: GeoGebra Tube
Sequências particulares
PA e função afim
Considere a PA (-1, 0, 1, 2, 3, 4, ...) de razão 1 e a função afim f(x) = 3x + 5. A sequência (f(-1), f(0), f(1), f(2), f(3), f(4), ...) também é uma PA.
f(-1) = 2
f(0) = 5
f(1) = 8
f(2) = 11
f(3) = 14
f(4) = 17
.
.
.
Observe que (2, 5, 8, 11, 14, 17, ...) é uma PA de razão 3. A razão dessa nova PA é o produto entre o coeficiente angular da função afim pela razão da PA anterior. Por fim, define-se:
Considerando a função f: R -> R e x1, x2, x3, x4, ..., xn, .... elementos de uma PA, f será uma função afim, definida por f(x) = ax + b, se, e somente se, f(x1), f(x2), f(x3), f(x4), ..., f(xn), ... for uma PA de razão a.r, sendo a o coeficiente angular de f e r a razão da PA inicial.
Exemplo 2 Seja a função afim f(x) = 4x - 2 e a PA (-6, -1, 4, 9, 14, 19, ...) de razão 5. A sequência (f(-6), f(-1), f(4), f(9), f(14), f(19), ...), dada por (-26, -6, 14, 34, 54, 74, ...) é uma PA de razão 20.
PG e função
Considere a PA (-2, 0, 2, 4, 6, 8, ...) de razão 2, e a função do tipo exponencial
. Verifica-se que a sequência (f(-2), f(0), f(2), f(4), f(6), f(8), ...) é uma PG (progressão geométrica).
f(-2) = 3/4
f(0) = 3
f(2) = 12
f(4) = 48
f(6) = 192
f(8) = 768
.
.
.
Se dividirmos cada termo Sn por Sn-1 descobrimos que esta é uma PG de razão 4.
A razão dessa PG é igual ao coeficiente a da função elevado à razão r da PA, ou seja, 
= 2² = 4.
= 2² = 4.Dados a função do tipo exponencial f: R-> R definida pore x1, x2, x3, x4, ..., xn, .... elementos de uma PA, a sequência (f(x1), f(x2), f(x3), f(x4), ..., f(xn), ...) é uma progressão geométrica (PG) de razão
Exemplo 3 Sejam a função exponencial f(x) = 3.(1/2)^x e a PA (-3, -1, 1, 3, 5, 7, ...) de razão 2, a sequência (f(-3), f(-1), f(1), f(3), f(5), f(7), ...), dada por (24, 6, 3/2, 3/8, 3/32, 3/128, ...) é uma PG de razão 1/4 = (1/2)².
Neste gráfico você pode manipular uma PG particular que possui domínio natural e lei de formação:
Fonte: GeoGebra Tube
Autor: Luiz Geraldo da Silva
Definindo sequências recursivamente
Sequências podem ser definidas recursivamente, ou seja, relacionando o n-ésimo termo aos termos anteriores e a todos os termos iniciais que forem necessários para se iniciar a sequência.
Exemplo 1
a) {1, 3, 7, 15, 31, 63...}
Cada termo dessa sequência corresponde a duas vezes o termo anterior mais 1. Por exemplo: 3 = 2.1 + 1, 7 = 2.3 + 1, ...
Então, uma possível equação para essa sequência é:
Também podemos reconhecer que as diferenças entre os termos consecutivos são potências de 2: 3 - 1 = 2, 7 - 3 = 4, 15 - 7 = 8, ...
Assim, podemos notar que cada termo corresponde a:
Sequências como casos particulares de funções
Uma sequência é uma função cujo domínio são os números inteiros positivos, ou seja, o conjunto 
(naturais), ou seja, 
. Pode-se, assim, entender uma sequência numérica como uma “seleção” de pontos de uma função de variável real.
(naturais), ou seja, 
. Pode-se, assim, entender uma sequência numérica como uma “seleção” de pontos de uma função de variável real.
Sequência de diferenças
Quando temos um termo an de uma sequência dependendo quantitativamente de n podemos, muitas vezes, construir o modelo matemático ou analisar esta dependência através das características variacionais destas variáveis, ou seja, o modelo é formulado através das variações destas grandezas. Entretanto, o termo variação pode ter diferentes formulações em matemática e para cada situação podemos escolher o tipo mais apropriado para o modelo. Nos exemplos acima, trabalhamos com o tipo mais simples de variação de uma sequência an, a variação simples (ou absoluta), que indicaremos por 
. Esses valores formam uma nova sequência ou função, que indicaremos por 
e denominaremos sequência de diferenças.
. Esses valores formam uma nova sequência ou função, que indicaremos por 
e denominaremos sequência de diferenças.Uma contextualização na Física
Seja S(t) a função horária de um objeto em movimento. Se soubermos os valores de "S" para valores inteiros de "t", tais como: S(0), S(1), S(2), S(3), S(4), ... teremos uma sequência simples. Dando um passo a mais, podemos construir uma sequência de diferenças ΔS, tal que ΔS = { S(1) - S(0), S(2) - S(1), ... }. Esses valores representam o deslocamento ou variação de posição entre 2 instantes consecutivos. Mas, perceba que S(1) - S(0) = ΔS/Δt, sendo Δt = 1. Logo, ΔS é também uma sequência de velocidades médias.
Exemplos:
i) Se um objeto está parado:
A sequência S é constante e ΔS = {0, 0, 0, ...}
Se um objeto está em M.U.:
No instante t + 1: 
S(t+1) - S(t) = V, constante, pois V não depende de t.
ii) Se um objeto está em M.U.V.:
No instante t: 
No instante t + 1: 
S(t+1) - S(t) = 
No caso do M.U.V., a velocidade não é constante ao longo do tempo. Logo, a velocidade média entre dois instantes consecutivos depende dos valores desses instantes.
Sequências com domínio inteiro
Vimos que uma sequência é uma função cujo domínio são os números inteiros positivos, ou seja, o conjunto lN (naturais), ou seja, 
. Podemos, no entanto, estender o conceito de sequências ou funções definidas em lN para funções definidas em Z (inteiros), ou seja, 
. Essas funções f com y = f(z) funcionam como “sequências estendidas”. Na figura 1 temos a representação da Z-função quadrática dada por 
, com z ∈ Z.
. Podemos, no entanto, estender o conceito de sequências ou funções definidas em lN para funções definidas em Z (inteiros), ou seja, 
. Essas funções f com y = f(z) funcionam como “sequências estendidas”. Na figura 1 temos a representação da Z-função quadrática dada por 
, com z ∈ Z.
Uma função diferença para Z-funções será dada por 
. Na figura 2 temos o gráfico da Z-função associada à função quadrática , com z ∈ Z.
. Na figura 2 temos o gráfico da Z-função associada à função quadrática , com z ∈ Z.
Algebricamente, temos:
Os valores de 
podem ser interpretados como a taxa da variação do gráfico de f entre os pontos (z, f(z)) e (z+1, f(z+1)). Geometricamente, os valores de 
correspondem à tangente do ângulo interno ao triângulo com vértices nos pontos (z, f(z)) e (z+1, f(z+1)). Seus catetos têm medidas |f(z+1) - f(z)| e Δz = 1.
podem ser interpretados como a taxa da variação do gráfico de f entre os pontos (z, f(z)) e (z+1, f(z+1)). Geometricamente, os valores de 
correspondem à tangente do ângulo interno ao triângulo com vértices nos pontos (z, f(z)) e (z+1, f(z+1)). Seus catetos têm medidas |f(z+1) - f(z)| e Δz = 1.
Questões para estudo deste conteúdo
