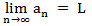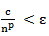Uma sequência converge
a um determinado valor se, a partir de certa posição, todos os seus termos estiverem
“tão próximos quanto queiramos” desse valor. Visualmente, seria como se
pegássemos um conjunto de réguas, daquelas que utilizamos na escola e, para
qualquer largura da régua, por menor que ela seja, existe uma posição a partir
do qual todos os pontos ficassem “dentro” da região delimitada pela régua, como
ilustrado a seguir.
Analisemos a sequência
como exemplo:
Como vimos no material
anterior, tomando o valor de n tão grande quanto queiramos, nossa sequência em
questão “aproxima-se”, converge para 1.
Uma definição provisória
para convergência de uma sequência pode então ser formulada:
Dada uma sequência an , dizemos que seu termos convergem a um determinado valor L, se ao tomarmos valores para n “bem grande” (o que indicaremos por "" - n tendendo ao infinito) existe uma posição, que aqui vamos chamar de n0, a partir da qual posso garantir que a distância entre os termos da sequência e o número L tornam-se tão pequenas quanto queiramos
Matematicamente podendo
ser representado:
Graficamente:
Nossos pontos centrais
seriam a representação da convergência da sequência a 1, a sequência de pontos
superiores (os quais não ultrapassam 1,5) e inferiores (nas proximidades de 1)
seriam a representação de nossa “régua”.
A sequência an converge para o número L se para todo número positivo ε existe um inteiro no natural tal
que, para todo n > no temos que | an - L | < ε.
Se esse número L não
existe, dizemos que an diverge. Se an converge para L, escrevemos:
e chamamos L de limite da sequência.
Exemplo 1 Considere a
sequência definida por 
, com c uma constante
real e p um número natural maior que 1. Vamos mostrar que 
.
, com c uma constante
real e p um número natural maior que 1. Vamos mostrar que 
.
Isso implica mostrar
que para
todo número positivo ε existe um inteiro no natural tal
que, para todo n > no, temos que | an - L | < ε, ou seja, 
.
.
Daí temos que 
, o que equivale a 
, ou ainda, 
.
, o que equivale a 
, ou ainda, 
.
Portanto, basta tomar 
.
. Somas parciais dos termos de uma sequência
Dada a sequência {an} podemos formar uma nova sequência {bn}, denominada sequência de somas parciais , tais que:
S1 = a1
S2 = a1 + a2
S3 = a1 + a2 + a3
...
Exemplo Calcular 
é equivalente a somar os cinco primeiros termos da PG com a1 = 1/2 e q = 1/2:
é equivalente a somar os cinco primeiros termos da PG com a1 = 1/2 e q = 1/2:
No caso dessa sequência, 
, temos que a sequência de somas parciais {Sn} será:
, temos que a sequência de somas parciais {Sn} será:
Essa sequência está convergindo e seu limite é 1.
No caso de uma PA, o matemático Gauss determinou uma fórmula para Sn tal que 
do seguinte modo.
do seguinte modo.
Para uma PG, temos Sn como 
, provado dessa maneira. Quando |q| < 1, temos que 
, o que mostra que a sequência se somas parciais converge.
, provado dessa maneira. Quando |q| < 1, temos que 
, o que mostra que a sequência se somas parciais converge.
Questões para estudo deste conteúdo
