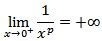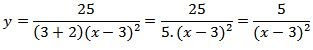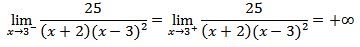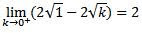3.2 Funções racionais e limites infinitos

Quando dizem que uma grandeza y é inversamente proporcional à outra, x, expressamos essa relação da forma , sendo k uma constante de proporcionalidade.

Por exemplo, se buscamos percorrer uma distância fixa, digamos k quilômetros, com velocidade constante, a relação entre a velocidade e o tempo é .

Funções desse tipo são casos particulares do que denominamos funções racionais (quociente de funções polinomiais).

Analisemos o gráfico da função racional "básica" :

Figura 1. Função racional mais simples possível, de relação .

Essa curva é formada por dois ramos, ilustrando o que denominamos descontinuidade essencial infinita, que manifesta a presença de uma assíntota horizontal (y = 0) e uma assíntota vertical (x = 0). Essas assíntotas são as retas das quais o gráfico de   se aproxima, à medida que tornamos os valores de x próximos a zero.

Note que, se  para valores tais que x > 0, então . Indicamos essa afirmação da seguinte forma:

Por outro lado, se  para valores tais que x < 0, então . Escrevemos, então, que:

Estamos aqui nos referindo aos chamados limites laterais.

Neste exemplo, temos que ambos os limites laterais não existem, pois a função cresce sem parar tanto para valores de x tendendo a zero pela esquerda, quanto pela direita.

De modo geral, se , temos:

i)                                      ii) 

Figura 2. Variações na função racional básica. Da esquerda para a direita, . Clique para ampliar cada imagem.

No caso de p par, o limite é bilateral e, portanto, escrevemos .

De maneira geral, dizemos que  se, para um número N > 0, existe f > 0 tal que se |x - a| < f, então f(x) > N.

No caso, podemos pensar que  se:

Portanto, tomando .

Geometricamente, dizemos que a reta x = a é uma assíntota vertical do gráfico de f se pelo menos uma das afirmativas a seguir for verdadeira:

Efeitos gráficos em 

Como apresentado no estudo de funções polinomiais, podemos alterar a lei da função por meio da utilização de determinados parâmetros, provocando alterações no gráfico como mostrados a seguir:

1) Translações horizontais (modifica-se a assíntota vertical);

De modo geral, sendo :

- Haverá translação horizontal para a direita, se c < 0.

- Haverá translação horizontal para a esquerda, se c > 0.

2) Translações verticais (modifica-se a assíntota horizontal);

De maneira geral, sendo :

- Haverá translação vertical para cima, se D > 0.
- Haverá translação vertical para baixo, se D < 0.

3) Contração e expansão;

Seja :

- Se A > 1, então a função se afasta da respectiva assíntota horizontal;
- Se 0 < A < 1, então a função se aproxima da respectiva assíntota horizontal;

3.1 Contração e expansão com reflexão;

A ideia é a mesma, porém, há o reflexo da função devido ao sinal. Veja:




Seja :

- Se A < -1, há reflexão e distanciamento da respectiva assíntota horizontal;
- Se -1 < A < 0, há reflexão e aproximação da respectiva assíntota horizontal;

Podemos aplicar esses efeitos gráficos no estudo de limites. Vejamos alguns exemplos:

Exemplo 1 

Observe que 

Ao expressarmos a função desse modo, identificamos uma sequência de efeitos gráficos:

i) translação da função  uma unidade para a direita;

ii) multiplicação por um fator 5;

iii) translação vertical da função duas unidades para cima.

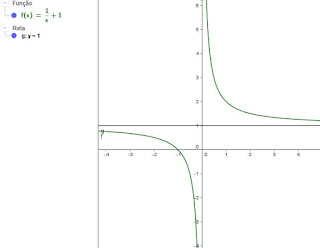
Graficamente, teríamos:

Figura 3. Gráfico da função . Em vermelho, a reta x = 1, assíntota única da função.

A reta x = 1 é assintótica à curva pois o valor 1 não está no domínio da função. Dessa forma, se x se aproxima de 1, temos:

Percebemos, também, que a função possui uma tendência para um valor constante de y. Podemos descobrir, então, sua assíntota horizontal com a seguinte manipulação algébrica:

Exemplo 2 

Há dois efeitos gráficos que podemos identificar na lei da função:

i) translação de 2 unidades para a direita;

ii) reflexão em relação ao eixo x devido ao fator -1 multiplicando.

Figura 4. Gráfico de .

A assíntota vertical da curva fica é a reta x = 2, pois observamos que:

E a assíntota horizontal permanece a reta y = 0, pois:

Exemplo 3 

Nesse caso não é possível, diretamente pela expressão, identificar todos os efeitos gráficos.

Essa função tem assíntotas verticais em x = -2 e x = 3, uma vez que nesses valores o denominador da função torna-se zero (e o numerador é constante, não dependendo de x).

Em x = -2, o valor do fator (x - 3)² é (-2 - 3)² = 25. Logo, próximo de x = -2, a função assemelha-se ao gráfico de

 

que é o gráfico de  deslocado duas unidades para a esquerda.

Assim,

Próximo de x = 3, temos:

ou seja, o gráfico de  deslocado 3 unidades para a direita.

Assim,

O gráfico de , considerando suas intersecções e assíntotas, é:

Figura 5. Gráfico de  e suas características. Em vermelho, as assíntotas x = -2 e x = 3. O ponto A é a intersecção da curva com o eixo y, ou seja, quando x = 0, y = 25/18 ≅ 1,39.

Integrais cujos integrandos têm descontinuidades infinitas

Se f é contínua em [a, b], exceto por uma descontinuidade infinita em a, a integral imprópria de f em [a, b] é definida por:

Como o limite existe, dizemos que a integral converge e o limite é definido como o valor da integral. Caso não exista, dizemos que a integral diverge.

Para uma descontinuidade infinita em b, a definição é:

Exemplo 1 

Resolvendo a integral e aplicando o limite:

Questões para estudo deste conteúdo

Download