Anteriormente, ao estudar sequências, investigamos como a sequência de diferenças pode fornecer informações a respeito do seu (de)crescimento, bem como a concavidade do seu gráfico.
Utilizando o conceito de limite em um ponto, podemos ampliar essa ideia. A derivada de uma função f é a função f ' tal que seu valor em qualquer número x' do domínio de f seja dado, se o limite existir, por:
Utilizando o conceito de limite em um ponto, podemos ampliar essa ideia. A derivada de uma função f é a função f ' tal que seu valor em qualquer número x' do domínio de f seja dado, se o limite existir, por:
Se x = a for um número do domínio de f, então
é a inclinação da reta tangente ao gráfico de y = f(x) no ponto (a, f(a)).
No applet abaixo você pode escolher uma função, por exemplo, f(x) = x³, e um valor x do domínio de f, deixando-o fixo. Movimentando o controle deslizante "h" e habilitando o rastro do ponto vermelho, você visualiza uma sequência de aproximações para o quociente 
, à medida que h tende a 0, tanto para x < 0 quanto para x > 0.
, à medida que h tende a 0, tanto para x < 0 quanto para x > 0.
Algebricamente, podemos confirmar este fato:
Para x = 3, então f '(3) = 3 . 3² = 27.
Considere agora a fórmula 
:
Se tomarmos (a + h) = x, então
é equivalente a 
, de modo que obtemos a seguinte fórmula para o cálculo de f '(a):
Como tarefa, mostre o resultado anterior agora usando esta fórmula!
Mais um exemplo: determinar f '(x) se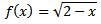
:
Para avaliar esse limite, vamos racionalizar o numerador:
Ficamos com:
Diferenciabilidade
Uma função é derivável em x = a se possui derivada em x = a, ou seja, existe
. Uma função será diferenciável em um intervalo aberto se for diferenciável em todo esse intervalo.
No primeiro exemplo anterior, f(x) = x³ é diferenciável para todo número real. Já no segundo exemplo, embora o domínio de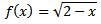 seja (-∞, 2], f é diferenciável em todo (-∞, 2], pois existe f '(2).
Seja agora
, função cujo domínio é toda a reta real.
Como
e
:Se tomarmos (a + h) = x, então
é equivalente a 
, de modo que obtemos a seguinte fórmula para o cálculo de f '(a):
Como tarefa, mostre o resultado anterior agora usando esta fórmula!
Mais um exemplo: determinar f '(x) se
:
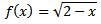Para avaliar esse limite, vamos racionalizar o numerador:
Ficamos com:
Diferenciabilidade
Uma função é derivável em x = a se possui derivada em x = a, ou seja, existe
. Uma função será diferenciável em um intervalo aberto se for diferenciável em todo esse intervalo.No primeiro exemplo anterior, f(x) = x³ é diferenciável para todo número real. Já no segundo exemplo, embora o domínio de
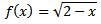seja (-∞, 2], f é diferenciável em todo (-∞, 2], pois existe f '(2).Seja agora
, função cujo domínio é toda a reta real.Como
e
então f não é derivável em x = 0.
Graficamente, o gráfico de f tem uma reta tangente vertical no ponto onde x é 0.
Clique sobre a imagem para ampliá-la. Note que g(x) = f '(x).
Tomemos agora f(x) = |x|. Seu domínio é toda a reta real.
Para x = 0, temos:
Se h > 0, então |h| = h. Daí 
Se h < 0, então |h| = -h. Daí 
Como os limites bilaterais são diferentes, f '(0) não existe. Note que no gráfico dessa função há um "bico" em x = 0.
Clique sobre a imagem para ampliá-la.
Ainda utilizando o applet anterior, tome para h algum valor suficientemente próximo de zero (mas diferente de 0). Com o rastro do ponto em vermelho habilitado, movimente o ponto x. O que você visualiza? Utilize as funções que analisamos algebricamente. Que relação há entre os cálculos que efetuamos e o comportamento geométrico observado? Pense a respeito.
As duas funções analisadas anteriormente, embora não fossem diferenciáveis em x = 0, eram contínuas em x = 0. Isso implica que o fato de uma função ser contínua em um ponto não automaticamente quer dizer que ela seja diferenciável nesse ponto. Mas, pode-se afirmar o seguinte:
Para provar esse resultado, precisamos mostrar que
ou, de modo equivalente, que 
.
Podemos re-escrever como 
e, aplicando a propriedade de limite de um produto, obtemos o seguinte:
As duas funções analisadas anteriormente, embora não fossem diferenciáveis em x = 0, eram contínuas em x = 0. Isso implica que o fato de uma função ser contínua em um ponto não automaticamente quer dizer que ela seja diferenciável nesse ponto. Mas, pode-se afirmar o seguinte:
"Se f é diferenciável em x = a, então f é contínua em x = a."
Para provar esse resultado, precisamos mostrar que
ou, de modo equivalente, que 
.Podemos re-escrever
como 
e, aplicando a propriedade de limite de um produto, obtemos o seguinte:
Regras de derivação
Podemos provar alguns resultados já instruídos geometricamente em outros momentos e também construir novas regras de derivação. Três resultados que já vêm sendo utilizados e podem ser provados são:
- A derivada de uma constante vezes uma função é a constante vezes a derivada da função, caso a derivada exista.
- A derivada da soma de duas funções é a soma de suas derivadas, caso elas existam.
- A derivada da diferença de duas funções é a diferença de suas derivadas, caso elas existam.
