Vimos anteriormente que, para algumas funções racionais, identificamos a existência de assíntotas verticais em valores de x para os quais o denominador da função tornava-se zero. Entretanto, se o numerador da função for também igual a zero nesses valores de x, o gráfico não terá assíntota vertical ali. Algumas técnicas de fatoração nos ajudam a entender o porquê.
Seja 
:
Note que f(1) não existe, uma vez que a razão 0/0 é indefinida. Porém, fatorando o numerador:
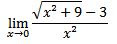
Note que, racionalizando o numerador:
Note que, como x = 0 pertence ao domínio de
, podemos dizer que 
.
De modo geral, se x = a pertence ao domínio de f(x),
.
Tal propriedade é satisfeita, por exemplo, por qualquer polinômio. Funções que satisfazem tal propriedade são ditas contínuas em x=a.
O estudo de funções modulares, em alguns casos, também leva a necessidade de trabalhar com limite.
Lembre-se que a função módulo (ou valor absoluto) é definida por:
Por exemplo:
Note que, para calcular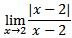
precisamos analisar separadamente os limites pela esquerda e pela direita:
O estudo do limite permite definirmos, de forma precisa, o conceito de continuidade. Intuitivamente, o gráfico de uma função pode ser descrito como uma curva contínua se não apresentar "quebras ou buracos". Isso não ocorre, por exemplo, com os gráficos de:
a)
(a curva separa-se em "dois ramos" devido á descontinuidade essencial infinita em x = 0);
b)
(a curva tem uma descontinuidade removível em x = 1);
c)
(há uma descontinuidade em salto em x = 2).
Dizemos que f é contínua em x = a se as seguintes condições forem satisfeitas:
i) f(a) está definida;
ii)
existe;
iii)
.
Nos três exemplos, temos que a condição (i) não é satisfeita, indicando a existência de uma descontinuidade em x = 0, em (a), em x = 1, em (b) e em x = 2, em (c).
Além disso, em (a) e (c), temos também que
não existem, de modo que a condição (ii) não é satisfeita.
Já em (b), temos que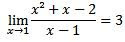
. Nessa caso, se definirmos a função como:
:Note que f(1) não existe, uma vez que a razão 0/0 é indefinida. Porém, fatorando o numerador:
Para todo x ≠ 1, podemos reescrever a função como y = x + 2. Logo, seu gráfico é uma reta y = x deslocada 2 unidades para cima, mas indefinida no ponto x = 1. A reta y = x + 2 contém o ponto (1, 3), mas o gráfico de f(x) não. Dizemos, então, que a função possui uma descontinuidade removível em x = 1.
Figura 1. Descontinuidade em (1, 3) removida de f(x) através da fatoração. Essa técnica é muito importante para fugir de indefinições em diversas funções racionais.
Utilizamos a notação 
para indicar o fato de que podemos tomar f(x) arbitrariamente próxima de 3 desde que tomemos x suficientemente próximo de 1, mas nunca igual a 1.
para indicar o fato de que podemos tomar f(x) arbitrariamente próxima de 3 desde que tomemos x suficientemente próximo de 1, mas nunca igual a 1.
Mais um exemplo:
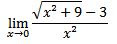
Note que, racionalizando o numerador:
Note que, como x = 0 pertence ao domínio de
, podemos dizer que 
.De modo geral, se x = a pertence ao domínio de f(x),
.Tal propriedade é satisfeita, por exemplo, por qualquer polinômio. Funções que satisfazem tal propriedade são ditas contínuas em x=a.
O estudo de funções modulares, em alguns casos, também leva a necessidade de trabalhar com limite.
Lembre-se que a função módulo (ou valor absoluto) é definida por:
Por exemplo:
Note que, para calcular
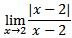precisamos analisar separadamente os limites pela esquerda e pela direita:
Então, se existe L tal que 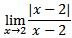= L, deveríamos ter L = 1 e L = -1. Como L não pode ter dois valores diferentes, L não existe. Dizemos que a função tem uma descontinuidade em salto em x = 2.
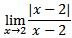= L, deveríamos ter L = 1 e L = -1. Como L não pode ter dois valores diferentes, L não existe. Dizemos que a função tem uma descontinuidade em salto em x = 2.Continuidade
a)
(a curva separa-se em "dois ramos" devido á descontinuidade essencial infinita em x = 0);b)
(a curva tem uma descontinuidade removível em x = 1);c)
(há uma descontinuidade em salto em x = 2).Dizemos que f é contínua em x = a se as seguintes condições forem satisfeitas:
i) f(a) está definida;
ii)
existe;iii)
.Nos três exemplos, temos que a condição (i) não é satisfeita, indicando a existência de uma descontinuidade em x = 0, em (a), em x = 1, em (b) e em x = 2, em (c).
Além disso, em (a) e (c), temos também que
não existem, de modo que a condição (ii) não é satisfeita.Já em (b), temos que
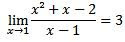. Nessa caso, se definirmos a função como:
Teremos que g(x) satisfaz as três condições em x = 1, implicando que g(x) é contínua em x = 1.
Se f é contínua em cada ponto do intervalo aberto (a, b), dizemos que f é contínua em (a, b). Além disso, se 
, dizemos que f é contínua no interval fechado [a, b].
Por exemplo, para todo x = a pertencente à (-3, 3), temos que:
Além disso,
, então dizemos que f é contínua em [-3, 3].
Um polinômio é uma função contínua em (-∞, +∞), ou seja, em toda a reta real. Uma função racional é contínua em todo ponto em que o denominador não se anula.
, dizemos que f é contínua no interval fechado [a, b].Por exemplo, para todo x = a pertencente à (-3, 3), temos que:
Além disso,
, então dizemos que f é contínua em [-3, 3].Um polinômio é uma função contínua em (-∞, +∞), ou seja, em toda a reta real. Uma função racional é contínua em todo ponto em que o denominador não se anula.
Questões para estudo deste conteúdo
