Logaritmos
Suponha que uma população cresça de acordo com a equação abaixo, onde t está em horas:
Quando esta população será de 2500? Desejamos resolver a seguinte equação para t:
Sabemos que 10³ = 1000 e 104 = 10000, então sabemos que 3 < t < 4, pois 1000 < 2500 < 10000. Mas como encontramos exatamente o valor de t para que P seja 2500? Para isso é que foi definida a função logaritmo comum (função log), escrita como  ou log x:
ou log x:
 ou log x:
ou log x:Se x é um número positivo, log x é o expoente de 10 tal que a potência resulta em x. Matematicamente, se
Por exemplo, log 100 = 2, pois 2 é o expoente de 10 tal que que a potência resulta em 100, ou seja, 10² = 100. Para resolver a equação  , devemos determinar a potência de 10 tal que essa potência resulte em 2500. Numa calculadora científica podemos utilizar a tecla "log" para estimar o valor de t. Encontramos:
, devemos determinar a potência de 10 tal que essa potência resulte em 2500. Numa calculadora científica podemos utilizar a tecla "log" para estimar o valor de t. Encontramos:
 , devemos determinar a potência de 10 tal que essa potência resulte em 2500. Numa calculadora científica podemos utilizar a tecla "log" para estimar o valor de t. Encontramos:
, devemos determinar a potência de 10 tal que essa potência resulte em 2500. Numa calculadora científica podemos utilizar a tecla "log" para estimar o valor de t. Encontramos:
Como previsto, este expoente está entre 3 e 4. O valor exato do expoente é log 2500; o valor aproximado é 3,398. Assim, leva aproximadamente 3,4 horas para que essa população alcance 2500.
LOGARITMOS SÃO EXPOENTES!
AS FUNÇÕES LOGARÍTMICAS E EXPONENCIAIS SÃO FUNÇÕES INVERSAS!
AS FUNÇÕES LOGARÍTMICAS E EXPONENCIAIS SÃO FUNÇÕES INVERSAS!
Para qualquer N,
e para N > 0,
O gráfico, o domínio e a imagem do logaritmo comum
O domínio de log x são todos os números positivos
Na figura acima podemos ver a imagem da função logarítmica. A curva cruza o eixo x em x = 1, visto que  = 0. O gráfico sobe para y = 1 em x = 10, pois log 10 = log (10¹) = 1. O gráfico de uma função logarítmica sobe tão lentamente depois de x = 1 que, para que y = 20, o valor de x deve ser
= 0. O gráfico sobe para y = 1 em x = 10, pois log 10 = log (10¹) = 1. O gráfico de uma função logarítmica sobe tão lentamente depois de x = 1 que, para que y = 20, o valor de x deve ser 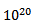 , ou 100 bilhões de bilhões! Por conta desse crescimento lento, essa função é utilizada frequentemente como padrão para outras funções com crescimento lento. Quando 0 < x < 1 ela cresce muito rapidamente, sendo assintótica em x = 0, mas nunca tocando o eixo y. Dessa forma, conclui-se que:
, ou 100 bilhões de bilhões! Por conta desse crescimento lento, essa função é utilizada frequentemente como padrão para outras funções com crescimento lento. Quando 0 < x < 1 ela cresce muito rapidamente, sendo assintótica em x = 0, mas nunca tocando o eixo y. Dessa forma, conclui-se que:
A imagem de log x são todos os números reais = 0. O gráfico sobe para y = 1 em x = 10, pois log 10 = log (10¹) = 1. O gráfico de uma função logarítmica sobe tão lentamente depois de x = 1 que, para que y = 20, o valor de x deve ser
= 0. O gráfico sobe para y = 1 em x = 10, pois log 10 = log (10¹) = 1. O gráfico de uma função logarítmica sobe tão lentamente depois de x = 1 que, para que y = 20, o valor de x deve ser 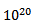 , ou 100 bilhões de bilhões! Por conta desse crescimento lento, essa função é utilizada frequentemente como padrão para outras funções com crescimento lento. Quando 0 < x < 1 ela cresce muito rapidamente, sendo assintótica em x = 0, mas nunca tocando o eixo y. Dessa forma, conclui-se que:
, ou 100 bilhões de bilhões! Por conta desse crescimento lento, essa função é utilizada frequentemente como padrão para outras funções com crescimento lento. Quando 0 < x < 1 ela cresce muito rapidamente, sendo assintótica em x = 0, mas nunca tocando o eixo y. Dessa forma, conclui-se que:O logaritmo natural
Quando e (número de Euler) é usado como base para funções exponenciais, os cálculos se tornam mais fáceis e, por isso, usamos uma outra função logarítmica, denominada logaritmo na base e. Esse logaritmo é tão frequente que possui notação própria: ln x, lido como logaritmo natural de x. Define-se:
Para x > 0,
ln x é o expoente da potência de e que resulta em x.
Matematicamente:
e y é denominado logaritmo natural de x.
Assim como as funções 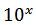 e log x são inversas, também são o
e log x são inversas, também são o  e o ln x. A função ln x tem propriedades similares à função logaritmo comum.
e o ln x. A função ln x tem propriedades similares à função logaritmo comum.
Propriedades do Logaritmo Natural
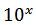 e log x são inversas, também são o
e log x são inversas, também são o  e o ln x. A função ln x tem propriedades similares à função logaritmo comum.
e o ln x. A função ln x tem propriedades similares à função logaritmo comum.Propriedades do Logaritmo Natural
ln 1 = 0 e ln e = 1.
- Para a e b ambos positivos e para qualquer valor de t,
ln (a/b) = ln a - ln b
ln ( ) = t . ln b
) = t . ln b

 ) = t . ln b
) = t . ln b
Funções exponenciais com base e representam crescimentos contínuos
Qualquer base positiva b pode ser escrita como uma potência de e.
Se b > 1, então k é positivo; se 0 < b < 1, então k é negativo. A função  pode ser escrita em termos de e:
pode ser escrita em termos de e:
 pode ser escrita em termos de e:
pode ser escrita em termos de e:
A constante k é denominada taxa de crescimento contínuo. Em geral:
Para a função exponencial, a taxa de crescimento contínuo, k, é obtida resolvendo
. Logo:

Se a for positivo,
- Se k > 0, então Q é crescente.
- Se k < 0, então Q é decrescente.
Como a nova fórmula representa a mesma função, queremos P = 175 quando t = 0. Logo, substituindo t = 0, resulta em  , então a = 175. O parâmetro a, em ambas as funções, representa a população inicial. Para todo t,
, então a = 175. O parâmetro a, em ambas as funções, representa a população inicial. Para todo t,
 , então a = 175. O parâmetro a, em ambas as funções, representa a população inicial. Para todo t,
, então a = 175. O parâmetro a, em ambas as funções, representa a população inicial. Para todo t,Portanto, k é o expoente da potência de e que resulta em 1,145. Pela definição de ln, obtemos:
k = ln 1,145 0,1354
Assim,
Outras aplicações
Acidez química
Os logaritmos são úteis para medir quantidades cujas magnitudes variam amplamente, tais como acidez (pH), som (decibéis) e terremotos (a escala Richter). Em química, a acidez de um líquido é expressa pelo pH. Ela depende da concentração de íons H+ (em mols/L) na solução, sendo esta concentração escrita como [H+]. Quanto maior for a concentração de H+, mais ácida é a solução. Por definição, o pH é:
pH = - log [H+]


Dessa forma, descobrimos que essa substância decai à uma taxa de 6,301 % por minuto, aproximadamente.
Utilizamos a regra da cadeia para demonstrar uma identidade de lnx.
Como , temos:
, temos:

Derivadas de funções logarítmicas e exponenciais
Derivada e integral da função logarítmica
Utilizamos a regra da cadeia para demonstrar uma identidade de lnx.Como
 , temos:
, temos:
Pela regra da cadeia:
Como 1/x é definido para todos os números reais (exceto o 0), temos que a integral desse polinômio é, pela demonstração acima:

Derivadas de funções logarítmicas e exponenciais
Exemplo 1
Como ln 1 = 0, a expressão anterior pode ser reescrita como:
ln|1| - ln|cosx| + C
E aí:
Exemplo 3: Integração por partes envolvendo função logarítimica











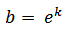





 0,1354
0,1354












