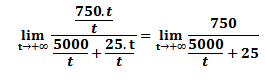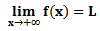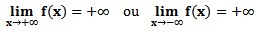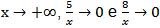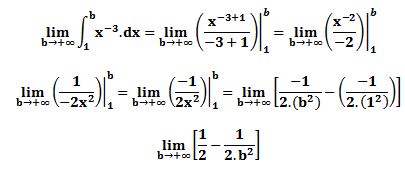Comportamento final de uma função
Considere um tanque que contém 5000 litros no qual são bombeados, por minuto, 25 litros de água contendo 750g de sais diluídos. A concentração de sais na água do tanque será dada por:
Onde t é o tempo, em minutos.
Podemos, a partir da função encontrada, determinar o comportamento da concentração de sais na água quando se tem valores de tempo muito grandes, ou seja, quando t→ +∞. Em notação de limite, temos que:
Dividindo o numerador e o denominador pelo maior grau de t, obtém-se:
Temos que ao fazermos t→+∞, a fração 5000/t → 0. Portanto:
Sendo assim, concluímos que a concentração tende a se estabilizar quando se assume valores muito grandes de t. Desta análise, chegamos à nossa definição informal de limites no infinito:
“Se f(x) assume valores tão próximos quanto queiramos de um valor L à medida que x cresce sem parar, então escrevemos 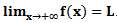 . Se f(x) assume valores tão próximos quanto queiramos de um número L à medida que x decresce sem parar, então escrevemos
. Se f(x) assume valores tão próximos quanto queiramos de um número L à medida que x decresce sem parar, então escrevemos  ”.
”.
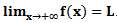 . Se f(x) assume valores tão próximos quanto queiramos de um número L à medida que x decresce sem parar, então escrevemos
. Se f(x) assume valores tão próximos quanto queiramos de um número L à medida que x decresce sem parar, então escrevemos  ”.
”.
A Figura 1 ilustra o gráfico das duas situações definidas. No primeiro caso, o valor de f(x) se aproxima da reta y = L à medida que x cresce; no segundo caso, o valor de f(x) se aproxima da reta y = L quando x decresce. Para estas situações, dizemos que a reta y = L é uma assíntota horizontal do gráfico de f(x).
Figura 1. Assíntotas horizontais.
Fonte: http://docplayer.com.br/docs-images/24/3910116/images/8-0.png
Para uma definição mais completa, precisamos garantir que existe um determinado valor de x a partir do qual a função f(x) estará dentro de um intervalo em torno da reta y = L, não importado quão pequeno este intervalo seja. Ou seja:
Seja f uma função definida em um intervalo aberto [a, +∞). Escrevemos:
Quando L satisfaz a seguinte condição:
Para qualquer ε > 0, existe A > 0 tal que |f(x) - L| < ε sempre que x > A.
Em outras palavras, existe um valor x = A tal que, para todo x > A, o valor da função f(x) estará contido em um intervalo [L - ε,L + ε].
Analogamente, seja f uma função definida em um intervalo aberto (-∞, b]. Escrevemos:
Quando L satisfaz a seguinte condição:
Para qualquer ε > 0, existe B < 0 tal que |f(x) - L| < ε sempre que x < B.
Podemos utilizar as definições acima para por à prova um importante teorema:
Se n é um número inteiro positivo, então:
Para demonstração do primeiro limite, devemos provar que para qualquer ε > 0, existe A > 0, tal que  sempre que x > A. Temos:
sempre que x > A. Temos:
 sempre que x > A. Temos:
sempre que x > A. Temos:
Desta forma,
O segundo limite pode ser demonstrado da mesma maneira e recomenda-se que o aluno desenvolva o mesmo durante seus estudos.
Outra possibilidade quando analisamos o comportamento final de uma função são os valores de f(x) crescerem ou decrescerem infinitamente quando x → ±∞. Para essas situações, dizemos:
Se os valores de f(x) crescem sem cota quando x → ±∞, então escrevemos,
conforme o caso.
Se os valores de f(x) decrescem sem cota quando x → ±∞, então escrevemos,
Se os valores de f(x) decrescem sem cota quando x → ±∞, então escrevemos,
conforme o caso.
Consideremos, para análise, o comportamento no infinito dos polinômios da forma 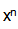 para n = 1, 2, 3 e 4. Graficamente (Figura 2), podemos notar que:
para n = 1, 2, 3 e 4. Graficamente (Figura 2), podemos notar que:
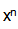 para n = 1, 2, 3 e 4. Graficamente (Figura 2), podemos notar que:
para n = 1, 2, 3 e 4. Graficamente (Figura 2), podemos notar que:
Note que a multiplicação de 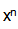 por um número real positivo não afeta os limites no infinito, entretanto, a multiplicação por um número real negativo provocará a inversão dos sinais.
por um número real positivo não afeta os limites no infinito, entretanto, a multiplicação por um número real negativo provocará a inversão dos sinais.
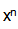 por um número real positivo não afeta os limites no infinito, entretanto, a multiplicação por um número real negativo provocará a inversão dos sinais.
por um número real positivo não afeta os limites no infinito, entretanto, a multiplicação por um número real negativo provocará a inversão dos sinais.
Para o caso de polinômios, há um princípio que afirma, de maneira informal, que o comportamento final de um polinômio coincide com o comportamento final de seu termo de maior grau. Ou seja:
Tal afirmação pode ser provada colocando em evidência o x de potência mais alta (no caso, 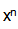 ) e examinando o limite da expressão fatorada. Assim,
) e examinando o limite da expressão fatorada. Assim,
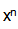 ) e examinando o limite da expressão fatorada. Assim,
) e examinando o limite da expressão fatorada. Assim,
Para determinarmos o comportamento final de uma função racional, uma estratégia é dividir cada termo do numerador e do denominador pela maior potência de x que ocorra no denominador.
Exemplo 1
Dividindo os termos pela maior potência de x, obtém-se:
Portanto,
Exemplo 2
Note que quando x → +∞, os termos
 tendem a zero. Assim,
tendem a zero. Assim, Os gráficos dos Exemplos 1 e 2 estão apresentados na Figura 3.
Figura 3. Gráficos das funções dos Exemplos 1 e 2.
Para este caso especial, onde a raiz está aplicada tanto no numerador quanto no denominador, a estratégia é calcular a raiz do limite e não o limite da raiz.
Partimos agora para o comportamento final da função:
A estratégia para este caso é manipular a função de modo que as potências de x se tornem potências de . Podemos, portanto, dividir o numerador e o denominador por |x|. Assim,
. Podemos, portanto, dividir o numerador e o denominador por |x|. Assim,
Portanto,
Nosso objetivo é determinar:
A estratégia para este caso é manipular a função de modo que as potências de x se tornem potências de
 . Podemos, portanto, dividir o numerador e o denominador por |x|. Assim,
. Podemos, portanto, dividir o numerador e o denominador por |x|. Assim,
Logo,
A mesma estratégia pode ser utilizada para determinar o comportamento da função quando x → -∞. Recomenda-se que o aluno efetue tal demonstração durante seus estudos.
4 Integrais sobre intervalos infinitos
Considerando uma função f que seja contínua e não negativa em um intervalo aberto [a,+∞), temos que a área sob a curva y = f(x) sobre o intervalo [a,+∞) será dada pela integral:
Figura 4. Área abaixo de y = f(x) definida no intervalo aberto [a, +∞).
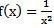 no intervalo [1,+∞).
no intervalo [1,+∞).Para calcularmos tal área vamos, inicialmente, calcular uma parte dela, para um intervalo fechado [1,b] com b > 1. Essa área será dada por:
Desenvolvendo os cálculos:
Substituindo os limites de integração:
Se permitirmos que b cresça de tal modo que b → +∞, então a área abaixo da curva e sobre o intervalo [1, b] irá começar a preencher a área sobre o intervalo [1, +∞). Portanto, podemos representar a área A sob
 sobre o intervalo [1, +∞) como sendo:
sobre o intervalo [1, +∞) como sendo:Conclui-se, portanto, que a área tem valor finito igual a 1, não sendo infinita como suposto inicialmente. A partir deste problema chegamos a mais uma definição:
A integral imprópria de f no intervalo [a,+∞) é definida por:
Caso o limite exista, dizemos que a integral imprópria converge e o limite é definido como sendo o valor da integral. Caso ele não exista, dizemos que a integral imprópria diverge e não é atribuído nenhum valor.
Exemplo 1
Reescrevendo a integral na forma de um limite:
Desenvolvendo a integral:
Fazendo b tender ao infinito:
Temos que o limite existe e, portanto, a área sob a curva
 no intervalo [1,+∞) é igual a 1/2.
no intervalo [1,+∞) é igual a 1/2.
Questões para estudo deste conteúdo