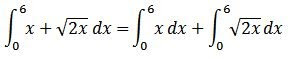Seja f(t) uma função contínua no intervalo a = t = b, os limites das somas pela esquerda e pela direita existem e são iguais. Dizemos que o limite dessas somas é a integral de f definida no intervalo [a,b]. Nota-se:
Mas por que o limite dessas somas é a integral definida da função? Ora, se tomamos n arbitrariamente grande, ou seja, se tendermos n ao infinito, teremos uma soma infinitesimal de retângulos nessa área. Assim:
e
.
O vídeo abaixo sintetiza nosso aprendizado sobre integrais até agora, confira antes de prosseguir para as propriedades dessa operação:
Propriedades da integral definida
É simples trabalhar com integrais uma vez que conhecemos suas propriedades. Dessa forma, cálculos de área tornam-se muito mais fáceis. Um exemplo bem claro de como as propriedades de integral (e claro, manipulações algébricas!) auxiliam nos cálculos pode ser visto nessa expressão:
Parece bastante complicada, mas ela se resume na seguinte integral:
Que é bem mais fácil de se resolver. Veremos agora todas as propriedades em detalhe. Suponha que f e g sejam funções contínuas.
Ordem dos limites de integração
Usualmente calculamos integrais definidas de um intervalo de a até b, sendo a < b. Porém, a definição de integral como o limite de uma soma de Riemann também vale para o caso contrário. Então, podemos dizer que:
Limites de integração iguais
Se a = b, então 
(pois não há variação). Então,
(pois não há variação). Então,
Integral de uma constante
É a constante multiplicada pelo intervalo. Isso porque o valor c da constante é a altura do retângulo e (b - a) a base do mesmo. Dessa forma:
Tome cuidado, pois a propriedade da soma e da diferença de integrais não se aplica para multiplicação e divisão!
Soma de integrais (também vale para a diferença!)
Quando temos duas ou mais funções dentro do mesmo integrando, então podemos dizer que:
Porque:
Tome cuidado, pois a propriedade da soma e da diferença de integrais não se aplica para multiplicação e divisão!
Integral de uma constante vezes a função Esta pode ser provada da mesma forma da soma das integrais acima, com propriedades de somatório. É uma das mais úteis propriedades na busca de funções primitivas.
Interpretações geométricas
Vamos utilizar as propriedades das integrais para resolver alguns exercícios. Como forma de conferir a resposta, introduza as funções no gráfico, onde:
f(x) = lei de f(x);
g(x) = lei de g(x);
h(x) = f(x) + g(x);
i(x) = f(x) . g(x);
i(x) = f(x) . g(x);
a = área sob f(x) até o eixo x;
b = área sob g(x) até o eixo x;
c = área sob h(x) até o eixo x;
d = área sob i(x) até o eixo x.
d = área sob i(x) até o eixo x.
Em negrito é o que você pode alterar no gráfico. O restante está embutido nos cálculos em função de f(x) e g(x). Por padrão, o intervalo a ser integrado é [0,6].
Fonte: GeoGebra Tube
Autor: Alan Couto
a) Verifique se:
- Plote f(x) = x e g(x) = sqrt(2x) (comando para o software entender raiz de 2x);
- Some as áreas a e b;
- Confirme que a + b = c.
b) Verifique se:
- Plote f(x) = x e g(x) = sqrt(2x);
- Multiplique as áreas a e b;
