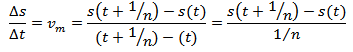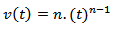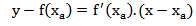O problema da velocidade instantânea
Sabemos a calcular a velocidade média de um objeto quando conhecemos as posições final e inicial desse objeto e o tempo que ele levou para sair da posição inicial e chegar à posição final. Sendo assim, a velocidade média deste objeto é dada por:
onde ΔS é a variação de espaço e Δt é a variação de tempo.
Como determinar, porém, a velocidade deste objeto em um determinado instante t? Em outras palavras, como determinar a velocidade instantânea de um objeto?
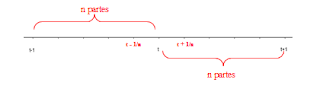
Uma estratégia é tomar intervalos de tempo cada vez menores em torno de t, tanto se aproximando pela esquerda quanto pela direita e calcular a velocidade média do objeto nestes intervalos.
Adotando, portanto, o instante t e dois intervalos, [t-1, t] e [t, t+1], e dividindo cada um deles em n partes temos a seguinte relação para a velocidade média.:
Para o intervalo à esquerda de t, temos:
Para o intervalo à direita de t, temos:
Para cada valor de n, obtemos uma estimativa da velocidade média para um intervalo de tempo 1/n. Temos então duas sequências que recebem o nome de sequência de quocientes de diferenças, pois são originadas a partir da divisão entre a diferença de posição do objeto pela diferença de tempo entre cada posição.
Queremos descobrir se as sequências obtidas convergem e, caso convirjam, se ambas convergem para o mesmo valor. Em outras palavras, deseja-se saber se existe 
e 
e se eles são iguais.
e 
e se eles são iguais.
Tomemos como exemplo a função S(t) = t² e o instante t = 1.
Obtidas as sequências de quocientes de diferenças podemos analisar sua convergência:
Para ambas o limite é 2t e, portanto, pode-se afirmar que a velocidade instantânea do objeto no instante t = 1 é 2. Ou seja, v(1) = 2.
Do desenvolvimento acima também concluímos que para um t qualquer, v(t) = 2t. As curvas de S(t) e v(t) estão apresentadas na Figura 1.
Figura 1. Representação gráfica das curvas s(t) e v(t).
Se tomarmos agora S(t) = t³, temos que a velocidade será dada por:
Aplicando o limite para analisar a convergência da sequência de quocientes de diferenças à direita, obtém-se:
Conclui-se, portanto, que a sequência converge para 3t². De forma análoga, mostra-se (como tarefa, desenvolva esses cálculos!) que obtemos o mesmo resultado se considerarmos a sequência de quocientes de diferença à esquerda.
Podemos chegar então a uma fórmula geral, no caso da posição ser uma função potência, ou seja, 
. Teremos então que:
. Teremos então que: 
Matematicamente, dizemos que:
Dizemos que a função velocidade é a derivada de S(t), em relação a variável t.
Sendo assim, seja um objeto que tem sua posição definida pela função S(t) = t³, a taxa de variação instantânea dessa função, ou seja, a velocidade instantânea deste objeto num instante t, será dada pela função v(t) = 3t².
Toda função derivada é, portanto, obtida a partir de uma sequência de quocientes de diferenças, e a velocidade instantânea é um caso particular disso: uma taxa de variação instantânea do espaço em função do tempo.
Essas taxas de variação aparecem em outros contextos como a taxa com a qual uma população muda com o tempo; a taxa com a qual o comprimento de um material muda com a temperatura; ou a taxa com que a o volume de um gás muda com a pressão.
Generalizando, dada y = f(x), podemos, para alguns casos, encontrar a sua derivada para um valor particular de x, que indicaremos por 
.
.
Sendo assim, para funções do tipo 
, temos que 
.
, temos que 
.
Geometricamente:
Figura 2. Reta secante aos pontos A e B.
Temos, geometricamente, que 
é a inclinação da reta secante aos pontos A e B (Figura 2). Dessa forma, 
é a inclinação da reta tangente ao gráfico da função no ponto A.
é a inclinação da reta secante aos pontos A e B (Figura 2). Dessa forma, 
é a inclinação da reta tangente ao gráfico da função no ponto A.
Sabendo-se que a equação de uma reta tangente é dada por 
Trazendo para o caso de y = f(x), temos:
Que representa a equação de uma reta que é tangente ao ponto A (Figura 3).
Figura 3. Reta tangente ao ponto A.
Algumas propriedades da derivada podem ser inferidas a partir da análise da inclinação da reta tangente, por meio do aplicativo abaixo:
1) Se c é uma constante, então 
, para y uma função potência;
, para y uma função potência;
2) Se y1 e y2 são funções potência, então 
.
.
A aplicação dessas duas propriedades possibilita calcular a derivada de qualquer função polinomial, ou combinações de funções potência que envolvem produto por constante e/ou somas e subtrações.
Questões para estudo deste conteúdo
